La culpa no es de los floats

Sino, del que le da de comer.

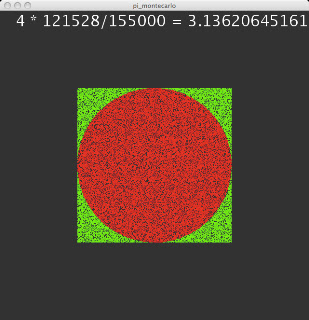
Al final del ultimo post, comenté mi preocupación por la lenta convergencia, y culpe apresuradamente al uso de los objetos de tipo float. 
Haciendo cuentas noté que no había nada raro en la convergencia.

El estimador era:
$$\tilde{\pi} = 4 * \frac{\sum^n_{t=1}I(\text{punto i esta dentro de circulo})}{n}$$
Esto se puede reescribir de la siguiente forma:
$$\tilde{\pi} = 4 * \tilde{F}$$ , donde $$\tilde{F} = \frac{\sum^n_{t=1}I(\text{1 si punto i esta dentro de circulo})}{n}$$ Sabemos que $I(\text{1 si punto i esta dentro de circulo})$ es una variable aleatoria Bernoulli, entonces
$\tilde{F} = \frac{Y}{n}$ donde Y es una variable Binomial con parámetros $n$ y $p = \pi/4$.
$$E[\tilde{\pi}] = 4 * \frac{E[Y]}{n} = 4 * \frac{\pi}{4} * n * \frac{1}{n} = \pi$$

Ahora, la varianza es lo que nos interesa.
$$\begin{aligned}Var[Y] &= np(1-p)\\ Var[\tilde{F}] &= \frac{np(1-p)}{n^2} = \frac{p(1-p)}{n} = \frac{\tilde{F}(1-\tilde{F})}{n}\\ Var[\tilde{\pi}] &= 4^2Var[\tilde{F}] = 8\frac{\tilde{F}(1-\tilde{F})}{n} \end{aligned}$$

Ahora, quiero generar un intervalo de confianza del $95\%$ (usando la normal, porque $n$ es muy grande), y quiero que ese intervalo tenga un tamaño del orden de $10^{-4}$. Teniendo la formula de la varianza del estimador, podemos calcular el $n$ para esa precisión: $n = 1035989708.4897318$. Acá queda claro que floats no tenía nada que ver con la falta de precision. Fue solo una cuestión de ansiedad.
De hecho, si usamos $n=10^9$, luego de un tiempito, tenemos el siguiente resultado


$$\tilde\pi = 3.141564804\, (3.67207693157*10^{-5})$$
y con un $\alpha = 5\%$ podemos construir el intervalo: $[3.14149283129\; 3.14163677671]$

Pi con Montecarlo

Hablando con tenuki sobre como usar montecarlo (ese pariente cercano a bootstrapping) para estimar objetos matematicos no aleatorios, me comentó que, por ejemplo, se podía estimar pi. De hecho, resultaba bastante facil hacerlo.
Imaginemos un cuadrado de lado 2, y dentro un circulo de radio 1. También pensemos en puntos que se distribuyen según una distribución uniforme dentro de ese cuadrado.
La probabilidad de que un punto esté dentro del circulo es pi/4 (la integral en el recinto definido por el circulo de f(x) = 1/area_del_cuadrado).
Una forma de estimar esta probabilidad es contando los puntos que estan dentro del circulo y dividir por n, lo que tiene como esperanza pi/4
Entonces, 4*puntos_dentro/total_puntos = pi

Es notable que la convergencia no es monotona, y puede tardar bastante en lograr buena precisión. Supongo que el uso de floats tiene algo que ver en el asuntó (en limitar la uniformidad de los puntos).